Quotient and Remainder Problem of Integers
The sum, difference and product of two integers are obviously integers but the quotient of two integers may or may not be an integer. For this reason, We say that – An integer ![]() is divisible by an integer
is divisible by an integer ![]()
![]() , if there is an integer
, if there is an integer ![]() such that
such that ![]() .
.
We denote this by ![]() and read as
and read as ![]() divides
divides ![]() . If no such integer can be found we write
. If no such integer can be found we write ![]() read as
read as ![]() does not divide
does not divide ![]() . Again
. Again ![]() then
then ![]() is called a divisor of
is called a divisor of ![]() and
and ![]() is called a multiple of
is called a multiple of ![]() .
.
On the other hand, if ![]() and
and ![]() then
then ![]() is called a proper divisor or factor of
is called a proper divisor or factor of ![]() .
.
Again ![]() . This shows that if
. This shows that if ![]() then
then ![]() . For practical purposes we can limit our attention to positive divisors of integers.
. For practical purposes we can limit our attention to positive divisors of integers.
Remember that ![]() is a divisor of any integer and
is a divisor of any integer and ![]() is a multiple of any integer. Any non zero integer is a divisor or a multiple of itself. A number which is a multiple of
is a multiple of any integer. Any non zero integer is a divisor or a multiple of itself. A number which is a multiple of ![]() is called an even number, otherwise it is called an odd number.
is called an even number, otherwise it is called an odd number.
THEOREM 1: For any integers ![]() the following hold
the following hold
-
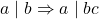 .
. -
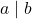 and
and 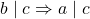 .
. -
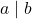 and
and 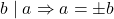 .
. -
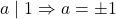 .
. -
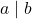 and
and 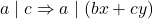 for any integers
for any integers 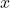 and
and 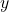 .
.
Proof:
- Given that,
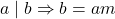 where m is any integer. Now
where m is any integer. Now 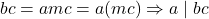 .
. - If
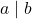 and
and 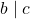 then there exist two integers
then there exist two integers 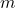 and
and 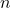 such that
such that 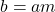 and
and 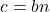 . Now
. Now 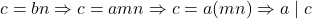 .
. - Given that
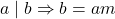 and
and 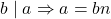 . From above those equations, we can write that
. From above those equations, we can write that 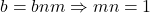 . Since
. Since 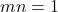 then both
then both 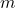 and
and 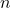 are
are 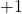 or
or 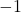 . Therefore
. Therefore 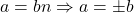 .
. - Given that,
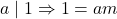 . Since
. Since 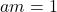 then both
then both  and
and 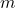 are
are 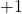 or
or 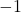 . Therefore
. Therefore 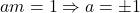 .
. - Given that,
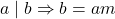 and
and 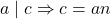 . Now
. Now 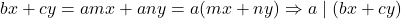 .
.
Now we discuss below about the theory of divisibility
THEOREM 2 (Fundamental theory of divisibility) : For any random pair of integers ![]() we always get another unique pair of integers
we always get another unique pair of integers ![]() such that
such that ![]() where
where ![]() .
.
Proof: Consider the infinite sequence of multiples of ![]() such that
such that ![]() . Obviously
. Obviously ![]() must be equal one of the multiples of
must be equal one of the multiples of ![]() say
say ![]() in the sequence or must be between two consecutive multiples say
in the sequence or must be between two consecutive multiples say ![]() and
and ![]() , for any arbitrary
, for any arbitrary ![]() . In either case, we have
. In either case, we have ![]() . Let
. Let ![]() . Since
. Since ![]() are integers then
are integers then ![]() also an integer that is
also an integer that is ![]() is an integer. Therefore
is an integer. Therefore ![]() . Hence the existence of
. Hence the existence of ![]() and
and ![]() are proved.
are proved.
Now we have to show that ![]() and
and ![]() are unique integers for
are unique integers for ![]() and
and ![]() . Let
. Let ![]() and
and ![]() aren’t unique integers for
aren’t unique integers for ![]() and
and ![]() . Then there exist
. Then there exist ![]() integers such that
integers such that ![]() and
and ![]() .
.
Therefore ![]() . But this is impossible. Since both
. But this is impossible. Since both ![]() and
and ![]() are positive integers and less than
are positive integers and less than ![]() . Therefore
. Therefore ![]() and
and ![]() are unique.
are unique.
Leave a Reply