To discuss about the convexity of set first we discuss about line segment. What is Line Segment? Let any two points ![]() and
and ![]() in
in ![]() . The set
. The set ![]() ,
, ![]() is called the line segment joining the points
is called the line segment joining the points ![]() and
and ![]() . The points
. The points ![]() and
and ![]() are called end points of this segment and for each
are called end points of this segment and for each ![]() , where
, where ![]() the points
the points ![]() is called an in-between points or internal points of the segment. The line segment joining the points
is called an in-between points or internal points of the segment. The line segment joining the points ![]() and
and ![]() will be denoted by
will be denoted by ![]() . The open line segment denoted by
. The open line segment denoted by ![]() ,
, ![]() . Therefore
. Therefore ![]() ,
, ![]() is called the closed line segment.
is called the closed line segment.
Now we discuss about convex combination. Convex combination is nothing but a universal definition of line segment. The convex combination of a set of ![]() points
points ![]() in a space
in a space ![]() is also a point
is also a point ![]() in the same space given by
in the same space given by ![]() where
where ![]() is real scalars and
is real scalars and ![]() for all
for all ![]() and
and ![]() . Always remember that convex combination is also a point.
. Always remember that convex combination is also a point.
Convex Set : A point set is said to be a convex set if the convex combination of any two points of the set is in the set. In other words if all points of the line segment joining any two points of the set is in the set then the set is known as convex set. A subset ![]() is said to be convex set if for each pair of points
is said to be convex set if for each pair of points ![]() in
in ![]() the line segment
the line segment ![]() is contained
is contained ![]() . In symbols a subset
. In symbols a subset ![]() is convex set iff (if and only if)
is convex set iff (if and only if) ![]() . Hyperplane, hyper sphere, convex hull , half space etc are examples of convex set.
. Hyperplane, hyper sphere, convex hull , half space etc are examples of convex set.
Hyperplane: A hyperplane in ![]() is a set
is a set ![]() of points given by
of points given by ![]() where
where ![]() is a row vector given by
is a row vector given by ![]() and not all
and not all ![]() and
and ![]() is an n component column vector. A hyperplane can be defined as a set of points which will satisfy
is an n component column vector. A hyperplane can be defined as a set of points which will satisfy ![]() . A hyperplane in two dimension is a line and in the three dimension is a plane.
. A hyperplane in two dimension is a line and in the three dimension is a plane.
Convex Function : Let ![]() be a function :
be a function : ![]()
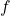 is said to be convex if
is said to be convex if 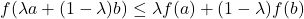 for all
for all 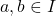 and all
and all 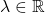 with
with 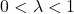 .
.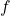 is said to be strictly convex if it is convex and the strict inequality holds in above mentioned equation
is said to be strictly convex if it is convex and the strict inequality holds in above mentioned equation 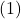 whenever
whenever 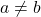 .
.
We may give some other equivalent, formulations of the convexity of function ![]()
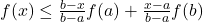 for all
for all 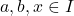 with
with 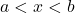 . Note that the right hand side of this enequality can be writen as
. Note that the right hand side of this enequality can be writen as 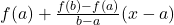 .
.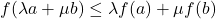 . For all
. For all 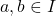 and all
and all 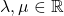 such that
such that 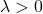 ,
, 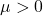 ,
, 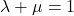 .
.
THEOREM : Let ![]() be convex. Then
be convex. Then ![]() . Whenever
. Whenever ![]() ,
, ![]() .
.
Proof : Since ![]() is convex, we have
is convex, we have ![]() . From this inequality we can derive
. From this inequality we can derive ![]() . Therefore
. Therefore ![]() which proves the first inequality of the theorem. The second inequality can be proved in a similar way.
which proves the first inequality of the theorem. The second inequality can be proved in a similar way.
Leave a Reply