Quadratic Equation
The general form of the quadratic equation is
![]()
It’s general solution is:
![]()
Where ![]() ,
, ![]() and
and ![]() are constant and
are constant and ![]() .
.
This equation, its solutions, and its graph are fundamental in various fields of science, engineering, and finance. It serves as a foundational topic in algebra and calculus courses around the world.
Extract the general solution from the Quadratic Equation:
Again the general form of the Quadratic Equation is
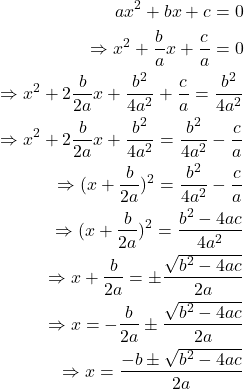
That means the quadratic equation has ![]() solutions or roots and let
solutions or roots and let ![]() and
and ![]() .
.
Now,
![]()
And
![]()
Thus the quadratic equation becomes
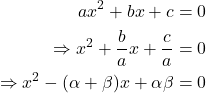
Which means if we know about the quadratic equation, we can find out it’s solutions and vice versa.
Now we discuss about the characteristics of the roots(solutions) of the quadratic equation
The term inside the square root ![]() is known as the discriminant and it determines the nature of the roots of the quadratic equation. Based on the value of the discriminant, the roots can have the following characteristics:
is known as the discriminant and it determines the nature of the roots of the quadratic equation. Based on the value of the discriminant, the roots can have the following characteristics:
-
Real and Distinct Roots (Two Different Real Roots):
When
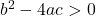 . The quadratic equation will intersect the x-axis at two distinct points. The graph will have two different x-intercepts.
. The quadratic equation will intersect the x-axis at two distinct points. The graph will have two different x-intercepts. -
Real and Equal Roots (One Real Root, also called a Repeated or Double Root):
When
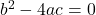 . Then the equation touches the x-axis but doesn’t cross it. The graph will have a single x-intercept (vertex touches the x-axis).
. Then the equation touches the x-axis but doesn’t cross it. The graph will have a single x-intercept (vertex touches the x-axis). -
Complex/Imaginary Roots (No Real Roots):
When
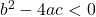 . It doesn’t intersect the x-axis at all. The graph has no x-intercepts and lies entirely above or below the x-axis. The roots are complex conjugates of each other and can be expressed in the form
. It doesn’t intersect the x-axis at all. The graph has no x-intercepts and lies entirely above or below the x-axis. The roots are complex conjugates of each other and can be expressed in the form 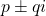 where
where 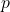 and
and 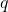 are real numbers.
are real numbers.
The quadratic equation and its associated quadratic function have a wide range of applications in various disciplines. Let’s explore some of these fields and how It plays a role:
Mathematics:
This is the most obvious field. Quadratic equations are foundational in algebra, helping students understand the nature of polynomial equations, graphing, and the properties of parabolas.
Physics:
In Projectile Motion The path of an object under the influence of gravity alone (ignoring air resistance) is a parabola which mathematical representation is Quadratic Equation. In Optics, The design and analysis of lens shapes directly involves quadratic equations. In Quantum Mechanics, The Schrödinger relation, which describes how the quantum state of a physical system changes in time, can be reduced to a quadratic form in certain situations.
Biology and Medicine
Quadratic equations can be used in modeling certain biological processes or phenomena, such as the spread of diseases or the growth of populations under certain assumptions.
Economics
The quadratic functions are used in various economic models, especially in the study of cost functions, revenue functions, and profit functions. The concept of diminishing returns in economics, where a variable reaches a point where the incremental benefit starts decreasing, can be modeled using it.
Engineering
In Structural Engineering, Analysis of certain structures, such as bridges or buildings, can involve solving quadratic equations. In Electrical Engineering, Quadratic equations arise when studying electrical circuits, especially in AC circuit analysis.
Computer Science
Algorithms that involve searching, sorting, or optimizing might utilize quadratics. Additionally, many algorithms related to graphics, animation, and game design use quadratic curves.
Finance
This equation can be used in various financial models. For instance, the calculation of compound interest, valuation of certain types of financial options, and optimization of investment portfolios.
Chemistry
Reaction kinetics, particularly when dealing with second-order reactions, can lead to quadratic equations. The equilibrium concentrations of reactants and products are determined by solving a quadratic equation.
Astronomy
When predicting the orbits of celestial objects or interpreting the light curves of stars, quadratic equations can come into play.
Geography and Geology
Studying certain types of terrain, erosion patterns, or the modeling of mineral extraction can lead to quadratic equations.
Environmental Science
Modeling pollution levels, the growth of species in response to environmental factors, or predicting changes in ecosystems due to human activities can involve quadratic equations.
Conclusion:
From ancient civilizations to the formulaic approach of modern world, the journey of the quadratic equation is intertwined with the broader story of mathematics itself.